Big-O Notation Explained

I remember hating my algorithms class in college, and Big-O notation was part of the reason. I just never got it. It seemed completely disjointed from anything I could possibly do in real life. If that’s you as well, here’s an explanation that should clear it up for you.

How much harder does something get as you increase your input?

An algorithm is just a series of steps for solving a problem.

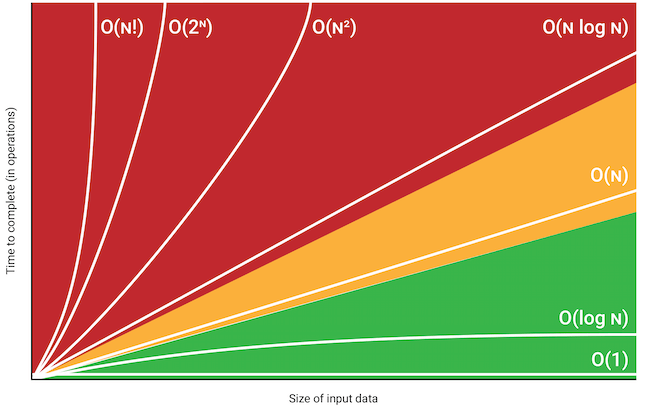
Big-O notation is a metric for algorithm scalability.

The entire point of Big-O notation is to be able to compare how efficiently one algorithm solves big problems compared to another.

So if you have a giant list of names, or phone numbers, or some other kind of input—what’s the best possible way of sorting them, or searching them, based on whether the list has 10 entries, or 100, or a million?

That’s what Big-O notation tells you. It tells you how well that particular approach will do against very large problems.

• 1 item, 1 second

• 10 items, 1 second

• 100 items, 1 second

Example: Determining if a binary number is even or odd.

It’s helpful to think of logarithms as exponents in reverse.

• 1 item, 1 second

• 10 items, 2 seconds

• 100 items, 3 seconds

Example: Binary search.

• 1 item, 1 second

• 10 items, 10 seconds

• 100 items, 100 seconds

Example: Unsorted list search.

Things raised to the second power are called quadratic because it comes from the Latin for "making square", i.e., to multiply times itself.

• 1 item, 1 second

• 10 items, 100 seconds

• 100 items, 10,000 seconds

Example: Bubble sort.

N! is a bad place in the algorithm world. It means it’s basically unsolvable.

• N=1, 1 option

• N=10, 3,628,800 options

• N=100, 9.332621544×10157 options

Example: Traveling salesman.

Summary

1. Algorithms are lists of steps for solving problems.

2. Some algorithms are good at problems when they’re small, but fail at scale, e.g., with very long lists of things to sort or search.

3. Big-O notation is the way to tell how good a given algorithm is at solving very large problems.

Notes

1. There are other Big-O notation types as well, but these are the major ones. Link