Our Constraints on Creativity
A list of different ways we limit ourselves creatively
This is some of my favorite, most popular, and latest content. You can also browse and search the archives.
A list of different ways we limit ourselves creatively

AI creates challenges that are specifically bad for VCs

Why the AI bubble argument misunderstands both bubbles and AI
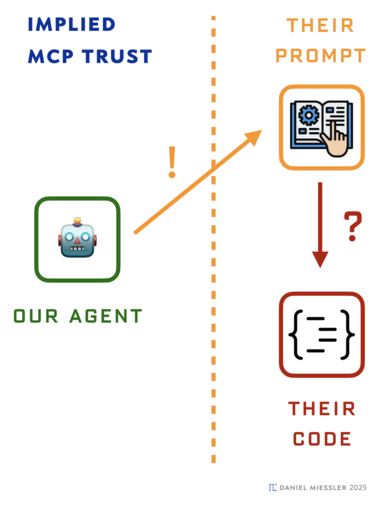
The trust interaction that happens between AIs during MCP operation

What do the people not getting laid off have in common?

How AI can transform us from workers into creators with the resources to be build our own ideas

Why we hold AI to impossible standards while giving humans a pass for the same limitations

Immediate concerns about the next few months and years