Diffie-Hellman

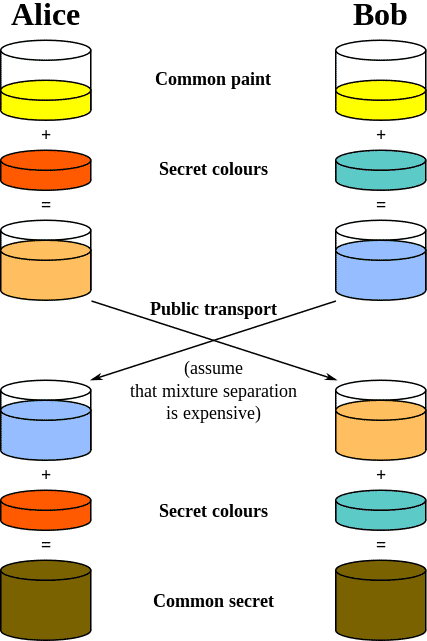
Diffie-Hellman is a key exchange protocol developed by Diffie and Hellman (imagine that) in 1976. The purpose of Diffie-Hellman is to allow two entities to exchange a secret over a public medium without having anything shared beforehand. As it turns out, this is an extremely important function, and understanding how Diffie-Hellman accomplishes this should be a point of interest for any information security enthusiast.

Basics

Two values, called Diffie-Hellman parameters, are at the core of this protocol, and they consist of a very large prime number p, and a second related “generator” number that is smaller than p, called g. The value for g is tied very strongly to its associated p value. The nature of this relationship is that for each number n, there is a power k of g such that n = g^k % p.

Each host must agree on these two parameters (p and g) in order for the protocol to work. Finally, a third and private value, called x is also generated for each host. This value, unlike p and g, is not shared.

Exchanges

Public values (to be exchanged with each other) are then generated with this function:

y = g^x % p

…or in other words, take value g and raise it to the power of value x, divide that by p, and your remainder is your public value y. Then, the two parties exchange their y‘s with each other and the exchanged numbers are used to create the shared secret z as follows:

z = y^x % p

…or, take the exchanged public key y and raise it to the power of your private key x, and divide that by the shared value p. The shared secret, z, is the remainder of that operation.

Results

The beauty of Diffie-Hellman is that after each party does this independently, they will both end up with the exact same value for z!. This means they now have an outstanding key for whatever encryption algorithm they decide on using for the rest of their communication.

This works because:

z = (g^x % p)^x' % p = (g^x' % p)^x % p

Unsupervised Learning — Security, Tech, and AI in 10 minutes…

Get a weekly breakdown of what's happening in security and tech—and why it matters.

Note that the portion of the equation above in parenthesis is the other host’s “public key”, and that it has the other host’s private value in it. This is what makes the arrival at a mutual secret possible mathematically.

So here’s how it breaks down:

1. Exchange some numbers over a public medium
2. Create your own private number that won’t be exchanged
3. Generate a public “key” from the previously agreed upon numbers combined with your private value
4. Perform a calculation using their public, your private, and the shared information
5. Your result will match that of your partner doing the same thing
6. You now have a shared secret without it ever crossing the public medium!

…or in other words, take the exchanged public key ‘y’ and raise it to the power of your private key ‘x’, and divide that by the shared value ‘p’. The shared secret, ‘z’, is the remainder of that operation.

The beauty of Diffie-Hellman is that both parties will end up with the same value for ‘z’! And ‘z’ makes an outstanding key for whatever encryption algorithm they decide on using for the rest of their communication.

This works because:

z = (g^x % p)^x' % p = (g^x' % p)^x % p

The key concept here is that the portion of the equation above in parenthesis is the other host’s public key. Notice that it has the other host’s private value in it. That’s what makes the attainment of a mutual secret possible mathematically.

The magic of Diffie-Hellman is that you not only end up with a shared secret, but the secret is never sent over the wire. Each side comes up with it independently, and that’s what makes the protocol so beautiful.